Metody numeryczne

Metoda ekstrapolacyjna Eulera

Rozwiązywane jest zagadnienie początkowe dy/dt = f(y, t) ,  y₀ = y(t₀) ,  

metodą ekstrapolacyjną Eulera     y_n+1 = y_n + h · f(t_n , y_n ) = y_n + h·y'_n,

gdzie: y₀ = y(0) - jest określone warunkiem początkowym, h - jest stałym krokiem całkowania, t_n= t₀ + n·h,   y_n = y(t_n) = y(t₀+ n·h). 

Dostępne funkcje: abs(x), acos(x), asin(x), atan(x), atan2(x,y) ceil(x), cos(x), exp(x), floor(x), log(x), pow(x,y), round(x), sin(x), sqrt(x), tan(x).
Dostępne stałe: E, PI, SQRT2, SQRT1_2, LN2, LN10, LOG2E, LOG10E.

Przykładowy obwód RC i równanie różniczkowe opisujace ten obwód.
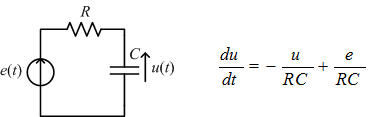