Metody numeryczne

Szybka transformacja Fouriera - FFT

Szybka transformacja Fouriera (ang. Fast Fourier Transformation – FFT), jest efektywna metodą obliczania dyskretnej transformacji Fouriera  (ang. Discrete Fourier Transform – DFT).

Dyskretna transformata Fouriera jest obliczana dla skończonej liczby N unormowanych pulsacji Ω_k = 2πk/N, k = 0, 1, 2, ... , N − 1. N punktowej dyskretnej transformacji Fouriera dokonuje się na skończonym ciągu x[n] o długości N i w wyniku uzyskuje N prążków widma sygnału

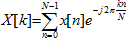  ,  k = 0, 1, 2, ... , N − 1.

Aby nie wprowadzać w obliczeniach numerycznych liczb zespolonych, część rzeczywistą transformaty można oznaczyć literą a, część urojoną literą b,  X[k] = a[k] + jb[k].

Gdy ciąg x[n] jest ciągiem rzeczywistym zachodzą związki symetrii  a[k] = a[N − k], b[k] = − b[N − k].

Ilość obliczeń potrzebnych do obliczenia DFT można zmniejszyć, gdy długość ciągu N jest całkowitą potęgą liczby 2, co jest wykorzystywane w FFT. Zwykle oznacza się N = 2^P, gdzie P jest liczbą naturalną.

Oblicznie DFT z wykorzystaniem biblioteki Math.Net Numerics

Do obliczania DFT ciągu zespolonego wykorzystuje się statyczną metodę FourierForward( klasy  MathNet.Numerics.IntegralTransforms.Transform.

Przykład wykorzystania metody nia metody FourierForward().

System.Numerics.Complex[] dane = new Complex[WYMIAR];

// Przygotowanie danych

MathNet.Numerics.IntegralTransforms.Transform.FourierForward(dane, MathNet.Numerics.IntegralTransforms.FourierOptions.Matlab);

W powyższym przykładzie dane są umieszczone w zespolonym wektorze dane.
W wyniku działania metody FourierForward(...)wektor zespolony dane zmienia zawartość na zespolone współczynniki DFT.

Aby przygotować dane dla metody FourierForward(...), powyższe sygnały należy spróbkować w punktach t_k = 2πk / N,  k = 0, 1, 2, ... , N − 1.